Retrouvez l'intégralité de ce billet sur Web.O.Toff
La Jolie Choucroute de l'année 2010 a été choisie, et la petite Keeley Hazell ne termine que 4ème :'(. En étudiant cette rétrospective de Choucroute, j'ai pu remarquer qu'il manquait dans le lot une certaine Kelly Brook. Si vous ne connaissez pas Kelly Brook, sachez que cette dernière a été désignée il y a quelques années par une étude scientifique comme ayant un corps parfait. Rien que ça ;p.
En effet, ce mannequin a fait l'objet en 2007 d'une étude minutieuse réalisée par des scientifiques spécialisés en morphologie. Ces derniers ont donc passé au crible chaque partie de son corps pour en conclure qu'elle était scientifiquement parfaite.

Après cette anecdote, qui je suis sûr, vous en touche une sans faire bouger l'autre, voici une petite galerie de la demoiselle en question. De son vrai nom Kelly Ann Parsons, Kelly Brook est née le 23 novembre 1979 à Chatham en Angleterre. En 2005 elle est élue la femme la plus sexy du monde par le magazine FHM.

A ce propos, sachez qu'en mathématiques et plus particulièrement en algèbre dans le contexte de la théorie de Galois, un corps parfait est un corps dont toutes les extensions algébriques sont séparables.Les corps parfaits sont utiles pour la théorie de Galois, car les théorèmes fondateurs, comme le théorème de l'élément primitif ou le théorème fondamental de la théorie de Galois utilisent dans les hypothèses le fait que l'extension considérée est séparable.
Les corps parfaits sont relativement fréquents, en effet, tout corps de caractéristiquenulle comme ceux des nombres rationnels, des nombres réels ou des nombres complexes sont parfaits. C'est aussi le cas des corps finis. Les corps parfaits sont relativement fréquents, en effet, tout corps de caractéristique nulle comme ceux des nombres rationnels, des nombres réels ou des nombres complexes sont parfaits. C'est aussi le cas des corps finis.
On peut donc définir les corps parfait de la manière suivante :
Soit K un corps et L une extension algébrique de K.
-
- Un corps K est dit parfait si et seulement si toutes ses extensions algébriques sont séparables.
Dire qu'une extension est séparable signifie que tout polynôme minimal d'un élément de L à coefficient dans K n'admet aucune racine multiple dans sa clôture algébrique.
Exemples : Tout corps de caractéristique nulle est parfait. Un corps de caractéristique nulle est un corps où la somme réitérée de l'unité n'est jamais égale à zéro. Ainsi les corps des nombres rationnels et ses extensions ainsi que le corps des nombres réels est parfait.

Cependant, tous les corps ne sont pas parfaits. Considérons 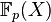 le corps des fractions rationnelles sur le corps fini de cardinal p, où p est premier, et Ω sa clôture algébrique. Si K est choisi comme étant égal à l'ensemble des fractions de
le corps des fractions rationnelles sur le corps fini de cardinal p, où p est premier, et Ω sa clôture algébrique. Si K est choisi comme étant égal à l'ensemble des fractions de  , alors K contient un polynôme non séparable. Considérons le polynôme P[X] de K[Y] égal à
, alors K contient un polynôme non séparable. Considérons le polynôme P[X] de K[Y] égal à  . Ce polynôme possède une unique racine X qui est donc un élément algébrique de degré p. De plus ce polynôme est irréductible. On en déduit que
. Ce polynôme possède une unique racine X qui est donc un élément algébrique de degré p. De plus ce polynôme est irréductible. On en déduit que 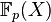 est le corps de décomposition du polynôme P[X]. Comme X est sa seule racine, P[X] n'est pas séparable.
est le corps de décomposition du polynôme P[X]. Comme X est sa seule racine, P[X] n'est pas séparable.
Source : Wikipédia.
Retrouvez l'intégralité de ce billet sur Web.O.Toff



